trvrm.github.io

Inspired by the keynote given at PyCon Portland by K Lars Lohn,, I wanted to try my hand at computing the fractal dimension of a few different images.

This is a very simple implementation of a box counting algorithm.

A couple of ideas are borrowed from https://github.com/twobraids/fracdim.

First some imports:

import pandas
import math
from IPython.display import display
from PIL import Image
import os
from  scipy.stats import linregress

Then a function to create simple black and white images.

def bw(img):
    gray = img.convert('L')
    return gray.point(lambda x: 0 if x<128 else 1, '1')

Some sample images. Basically, I expect the fractal dimension of the Canadian coastline to be higher than that of, say, a square.

texas=bw(Image.open('./images/texas.gif'))
tree=bw(Image.open('./images/tree.jpg'))
canada=bw(Image.open('./images/Canada.png'))
square=bw(Image.open('./images/square.jpg'))

At various different scales, I want to divide each image up into squares and then count how many squares have at least one black pixel in them.

def interesting(image):
    #true if any data is 0, i.e. black
    return 0 in set(image.getdata())

This function chops an image up into

def interesting_box_count(image, length):
    width,height=image.size

    interesting_count=0
    box_count=0
    for x in range(int(width/length)):
        for y in range(int(height/length)):
            C=(x*length,y*length,length*(x+1),length*(y+1))

            chopped = image.crop(C)
            box_count+=1
            if (interesting(chopped)):
                interesting_count+=1        

    assert box_count
    assert interesting_count
    return interesting_count

This returns pairs of numbers. One represents the scale, the other the (log) count of boxes at that scale that have black pixels in them.

def getcounts(image):
    length=min(image.size)
    while(length>5):
        interesting = interesting_box_count(image,length)
        yield math.log(1.0/length), math.log(interesting)
        length=int(length/2)

def counts(image):
    return pandas.DataFrame(getcounts(image),columns=["x","y"])

def dimension(image):
    frame=counts(image)
    return linregress(frame.x,frame.y)

And finally, armed with lists of pairs, we compute the slope we'd get if we plotted them against each other.

def analyse(image):
    c=counts(image)
    print("Fractal Dimension:",linregress(c.x,c.y).slope)

Results

square

png

analyse(square)

Fractal Dimension: 1.26420823227

texas

png

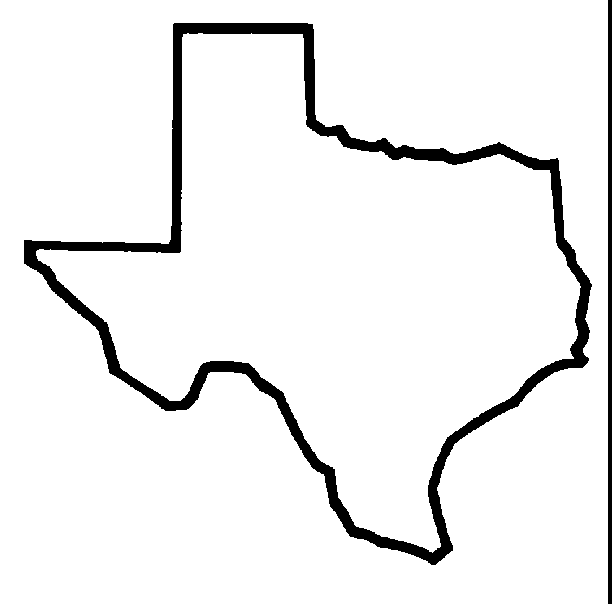
analyse(texas)

Fractal Dimension: 1.45764518178

canada

png

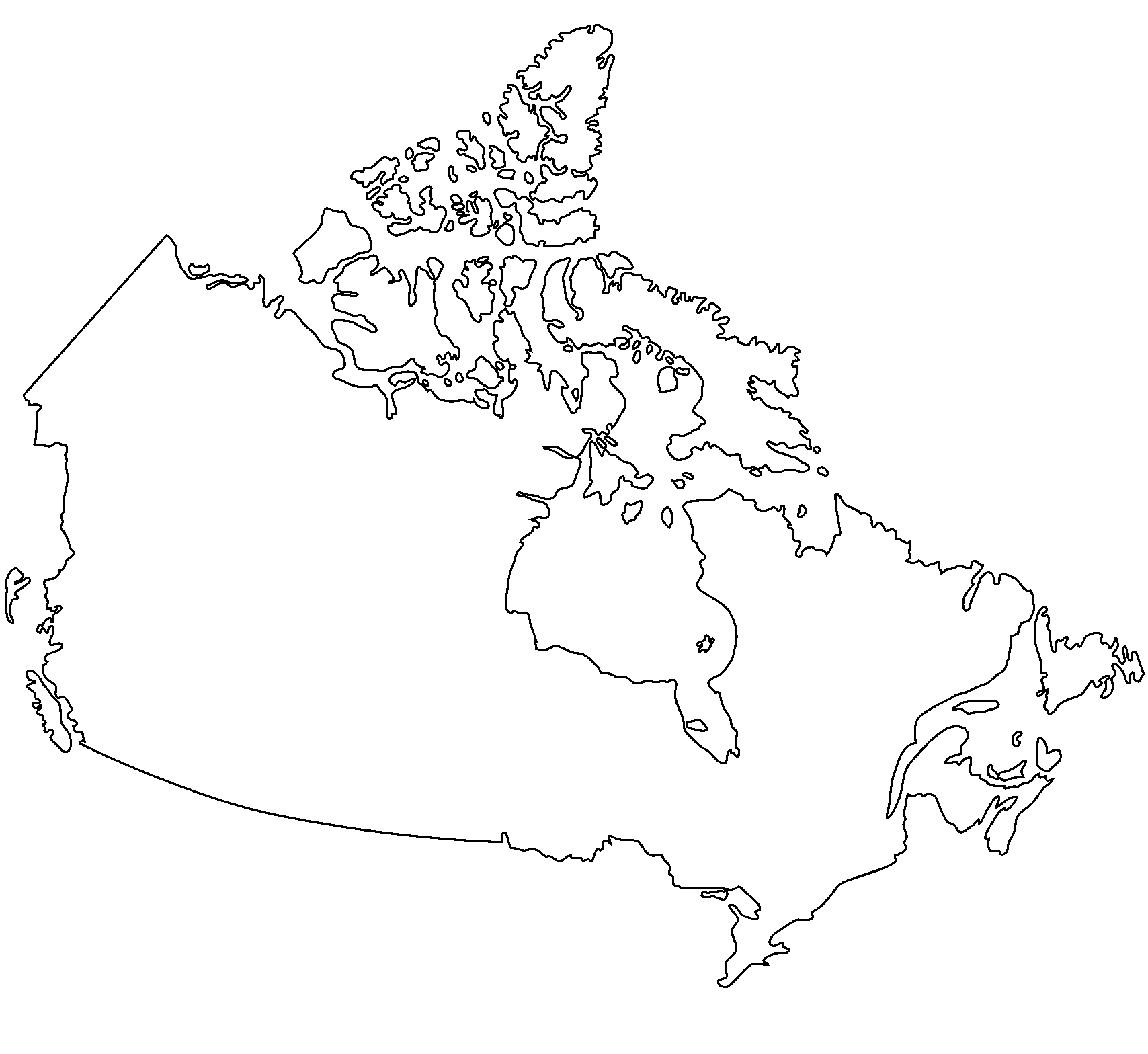
analyse(canada)

Fractal Dimension: 1.52450994232

tree

png

analyse(tree)

Fractal Dimension: 1.82487974473

Which is exactly what we expected.

As K Lars Lohn said in his keynote, it's very rewarding when you try something out in Python and the result actually matches neatly up with the theory!